Editor’s Note: In this new column, Dr. Craig Johnson, professor of mathematics and computer science, will discuss topics related to our use of math in everyday life.

Last fall, we witnessed another close presidential election in which the popular vote winner did not succeed in winning the election. The 2016 contest was one of the most unusual and contentious in American history.

As in many prior elections, it has again given impetus toward a re-examination of the very voting method that our nation employs to select its leaders. People of every political stripe would probably agree that it is in keeping with the basic tenets of democracy to use the method that best reflects the aggregate will of the voting populace.

Much research has been done in the last 30 years that shows that replacing our current long-standing plurality method- vote for one, most votes wins- could not only better meet the voters’ will, but might also reduce the vitriolic rhetoric of a hard-fought campaign.

Alternate methods do exist and, in fact, are currently used in this country and elsewhere to decide other types of elections ranging from mayoral races in some of the largest cities to awards for the “Most Valuable Player” or “Rookie of the Year” in most major sports leagues.

Some democracies in the world, like Australia, Ireland, India and Scotland, also have successfully used alternate voting schemes called that most experts believe gauge voter sentiment far more accurately than the plurality method.

The remarks here do not address the pros or cons of the Electoral College that gets scrutinized every four years by the post-election pundits with no effort ever initiated toward changing it. Rather, this discussion is about the way we mark the ballots themselves.

Instead of being limited to voting for just one candidate, consider the possibility of each voter ranking the candidates: #1 for his/her favorite, #2 for the next favorite and so forth.

The example below represents a ballot where voters number the candidates in order of preference.

Graphic credit/ Katlynn Whitaker

In the field of social choice, these types of ballots are called preference ballots and a variety of methods exist by which to tabulate them.

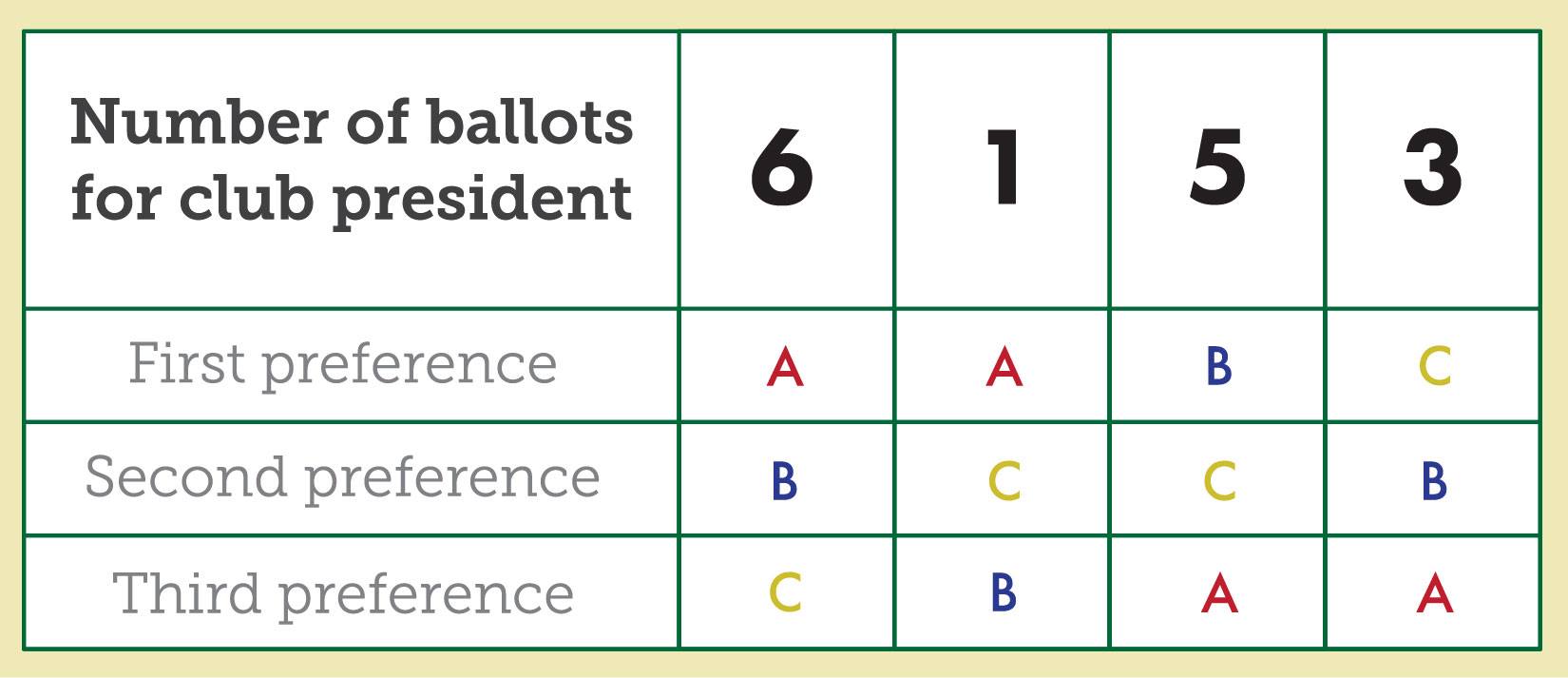
For example, suppose the Marywood Ski Club held an election for club president among Alicia, Barzhon and Carlos and that the 15 members used preference ballots. The following table, called a preference table, summarizes the results. Let “A” represent the ranking for Alicia, “B” represent Barzhon and “C” represent Carlos.

Graphic credit/ Katlynn Whitaker

This table indicates that six voters voted for Alicia first, Barzhon second and Carlos third. Only one voter ranked Alicia first, Carlos second and Barzhon third.

Alicia would win this election by the plurality method—the same method used to elect our president—because she received seven votes for first place.

However, the Borda Method, which is used in determining the Heisman Trophy and many other sports awards, assigns three points for each first place vote, two points for every second place vote and one point for every third-place vote. You can verify that the Borda count for each candidate is:

Alicia: 7(3) + 0(2) + 8(1) = 29

Barzhon: 5(3) + 9(2) + 1(1) = 34

Carlos: 3(3) + 6(2) + 6(1) = 27

Barzhon wins the election instead of Alicia if the Borda Method is used. An examination of the table shows this perhaps corresponds to the fact that Alicia was ranked last by eight voters whereas Barzhon was ranked second by nine voters and last by only one.

By the Borda Method, Barzhon seems to be a more agreeable choice to most of the members of the club even though he ranked at the top of fewer ballots than Alicia. One advantage is that voters whose second choice was the eventual winner would most likely not be wholly unsatisfied with that result.

The Borda method has another distinct advantage for presidential elections in that it encourages voter turnout by fans of third party candidates. They can still rank their underdog first, but place their next favorite candidate in second place.

When using this method, a person’s vote is not “wasted.” I heard from many students who did not vote in this recent election for that very reason. They knew that a vote for Gary Johnson or Jill Stein would not affect the outcome of the election.

The Nobel Prize-Winning Economist Kenneth Arrow devised a number of criteria for judging the fairness of any voting method and concluded that no system is perfectly fair, although some come closer than others. The plurality method, in particular, has many flaws when examined closely and the time to re-examine its effectiveness is long overdue.

Contact the writer: [email protected]